Алгоритмы распределения случайных величин

Равномерное распределение

Распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна.

                                                            

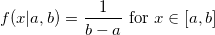
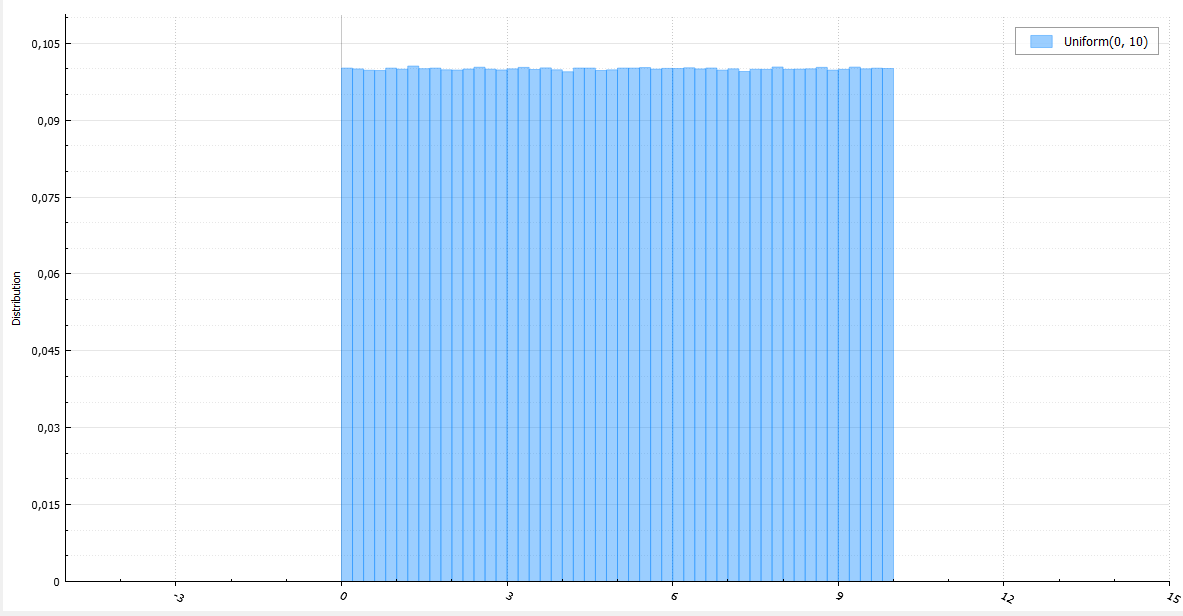
Равномерное распределение может использоваться при генерации почти что любой случайной величины.

Нормальное распределение

Распределение вероятностей, которое играет важнейшую роль во многих областях знаний. Случайная величина подчиняется нормальному закону распределения, когда она подвержена влиянию большого числа случайных факторов, что является типичной ситуацией в анализе данных. Поэтому нормальное распределение является хорошей моделью для многих реальных процессов.

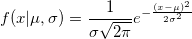
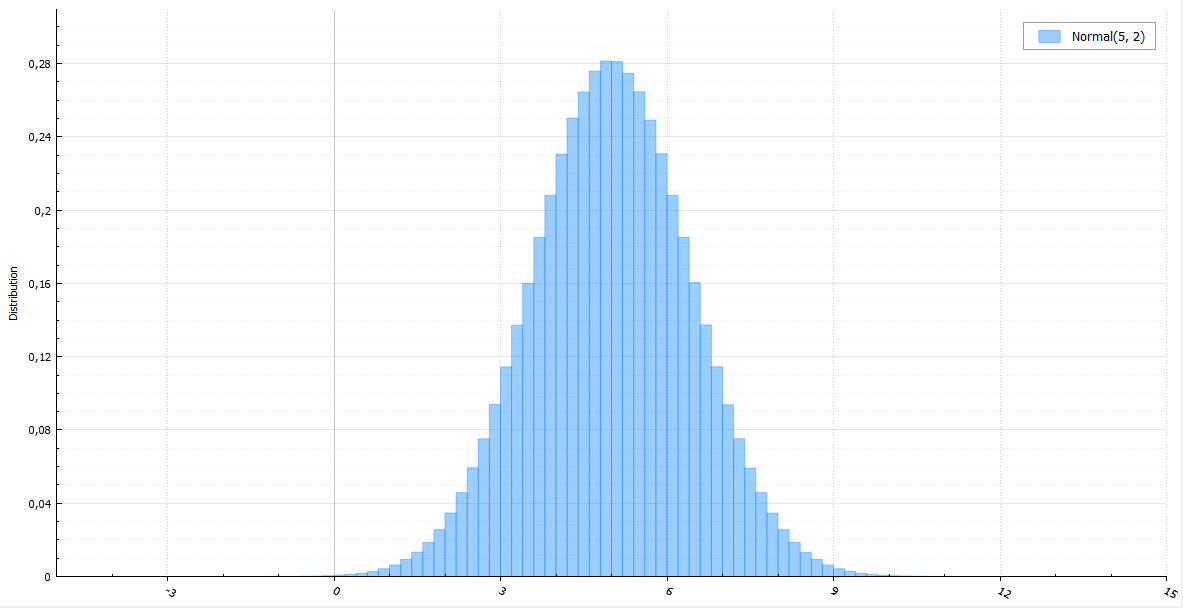
Смысл нормального распределения становится понятен из его формы. Наиболее вероятные значения случайной величины расположены вблизи его пика (среднего). По мере удаления от него, вероятность значений уменьшается и если значение расположено в «хвосте» распределения, то оно очень маловероятно.

Если исследуемый процесс подчиняется нормальному закону распределения (о чем принимается соответствующая статистическая гипотеза, проверяемая по различным критериям), то его статистический анализ существенно упрощается. В частности, предположение о нормальности распределения коэффициентов регрессии используется в регрессионных моделях, а в простом классификаторе Байеса – предположение о нормальности распределения непрерывных атрибутов, на основе которых производится классификация.

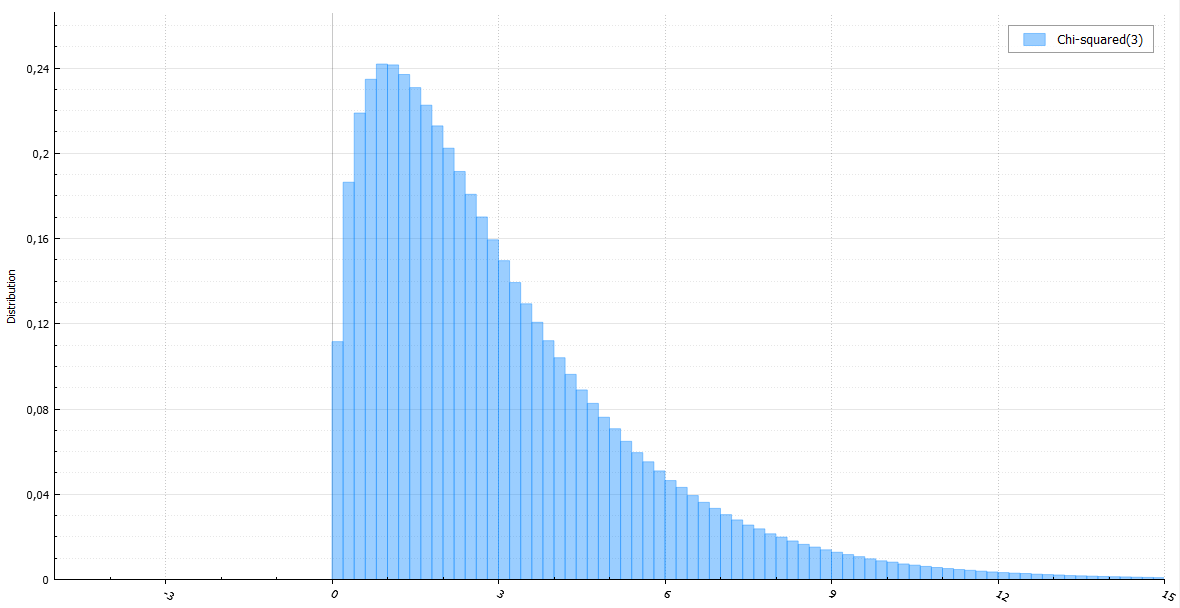
Экспоненциальное распределение

Абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события

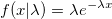
Экспоненциальное распределение описывает интервалы времени между независимыми событиями, происходящими со средней интенсивностью . Количество наступлений такого события за некоторый отрезок времени описывается дискретным распределением Пуассона. Экспоненциальное распределение вместе с распределением Пуассона составляют математическую основу теории надёжности.

Кроме теории надёжности, экспоненциальное распределение применяется в описании социальных явлений, в экономике, в теории массового обслуживания, в транспортной логистике — везде, где необходимо моделировать поток событий.

Экспоненциальное распределение является частным случаем распределения хи-квадрат (для n=2), а следовательно, и гамма-распределения. Так-как экспоненциально распределённая величина является величиной хи-квадрат с 2-мя степенями свободы, то она может быть интерпретирована как сумма квадратов двух независимых нормально распределенных величин.

Гамма-распределение

Это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр k принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрланга.

Гамма распределение широко применяется для моделирования сложных потоков событий, сумм временных интервалов между событиями, в экономике, теории массового обслуживания, в логистике, описывает продолжительность жизни в медицине. Является своеобразным аналогом дискретного отрицательного биномиального распределения.

Гамма-распределение является обобщением распределения хи-квадрат и, соответственно, экспоненциального распределения. Суммы квадратов нормально распределённых величин, а также суммы величин распределённых по хи-квадрат и по экспоненциальному распределению будут иметь гамма-распределение.

Гамма-распределение является распределением Пирсона III рода. Область определения гамма-распределения — натуральные неотрицательные числа.

Распределение Коши

Распределение Коши описывает отношение двух нормально распределенных случайных величин. В отличие от других распределений, для распределения Коши не определены матожидание и дисперсия. Для описания распределения используются коэффициенты сдвига  и масштаба .

Распределение Коши является бесконечно делимым: сумма независимых случайных величин, распределённых по Коши, также распределена по Коши.

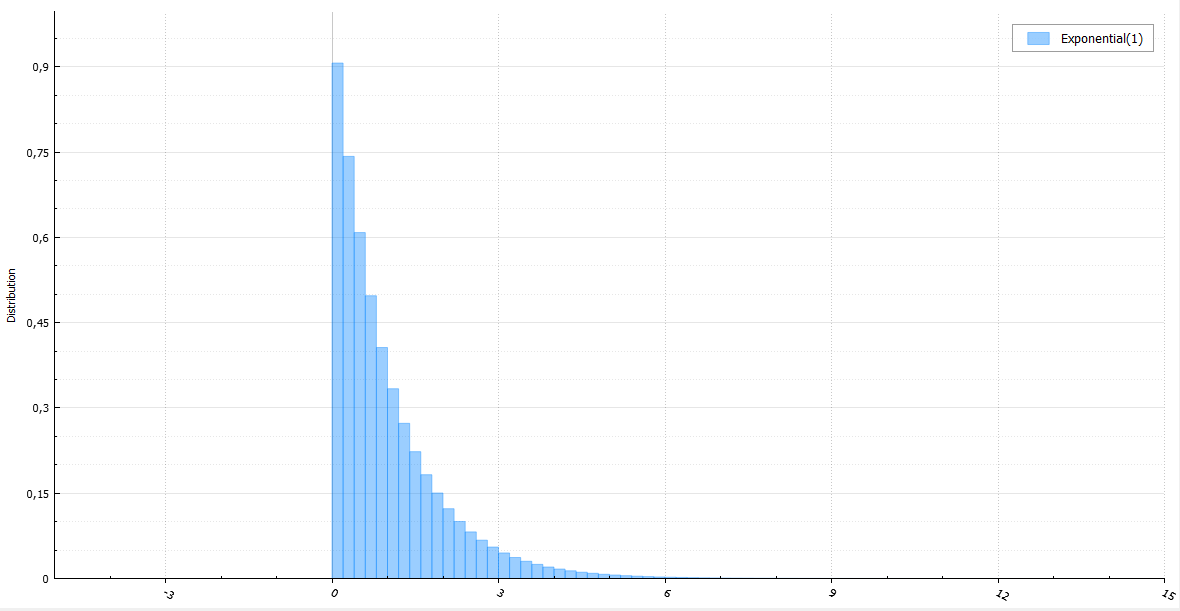
Распределение Лапласа

Распределение Лапласа — это то же экспоненциальное, только со случайным знаком. 

Распределение Леви

Распределение, которое может быть получено как предел по распределению сумм независимых случайных величин.

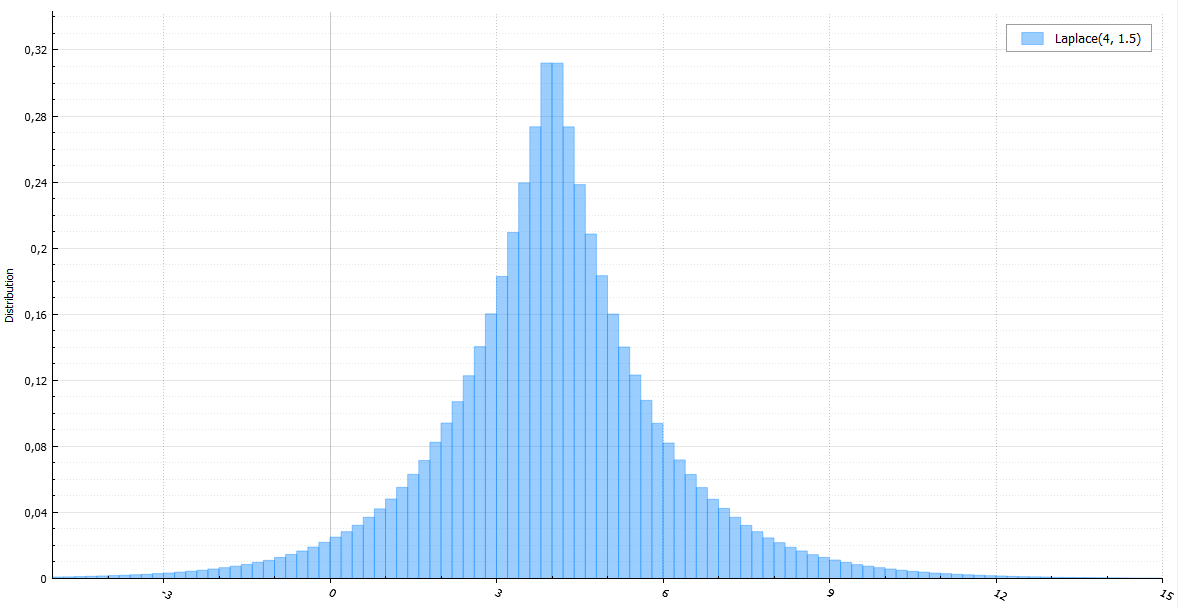
Распределение хи-квадрат

 является частным случаем гамма-распределения (а следовательно, распределением Пирсона типа III) и обобщением экспоненциального распределения. Отношение величин, распределенных по распределено по Фишеру.

На распределении  основан критерий согласия Пирсона. с помощью этого критерия можно проверять достоверность принадлежности выборки случайной величины некоторому теоретическому распределению.